Quantum computing is an emerging technology that employs the laws of quantum mechanics to perform computations.
Quantum computing is an emerging technology that employs the laws of quantum mechanics to perform computations.
While classical computers operate using binary bits which can only be in a single state – either “0” or “1” – quantum computers operate using qubits (quantum bits), which can be in a superposition of both “0” and “1” at the same time.
This property allows a quantum computer to perform computations in parallel. As a result, quantum computers can solve certain problems much faster than classical computers.
Given recent breakthroughs in quantum science and technology, we wanted to investigate the potential applications for quantum computing in the field of airline revenue management (RM). To do so, Amadeus partnered with the Danish companyKvantify , which specializes in quantum algorithms and high-performance computing. We presented our findings at theAGIFORS 2023 Revenue Management Study Group, held in Helsinki June 5th-7th , where our joint presentation on “Application of quantum computing in airline revenue management” received the award for Best Innovation.

What problems can be solved with today’s quantum computers?
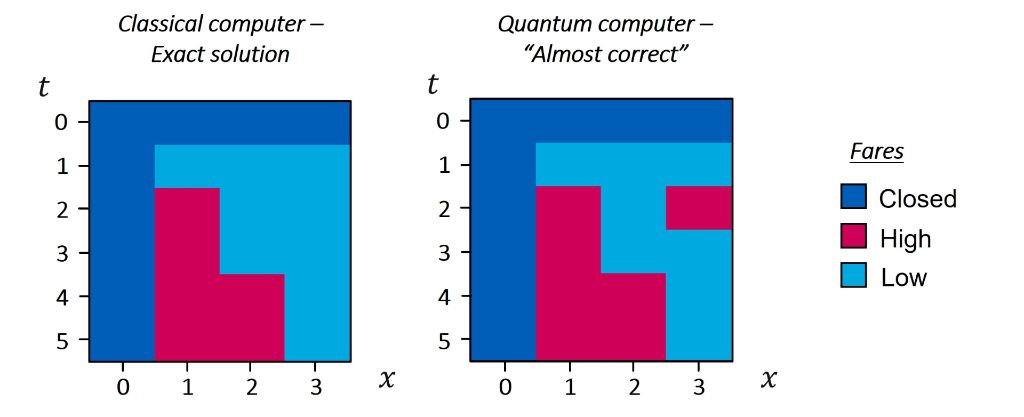
We started by evaluating whether the core problem of airline RM – the single flight leg optimization problem – could be solved using the quantum hardware that exists today. The solution to this problem can be expressed as a matrix that specifies the fare (price) for a flight depending on the remaining capacity (x) of the aircraft and the remaining time (t) to departure. This problem is routinely solved by all airlines and provides us with a benchmark to assess the output of the quantum computer.
The exact solution from a classical computer is illustrated in Figure 1 (left), where each colored square represents the fare that should be charged – high, low, or closed – depending on x and t. Note that the flight capacity here is only 3 seats. As it turns out, this small problem is the best we can do with the quantum hardware that exists today.
To solve this problem on a real quantum computer, we needed to develop a quantum algorithm to represent the problem. The quantum computer we chose was restricted to solving one problem type only:the Ising Model
, a mathematical model of magnetism. Therefore, we needed somehow to convert our airline RM problem into the language of magnets. Not that obvious!
However, we succeeded and the solution from the quantum computer is displayed in Figure 1 (right).
Comparing the matrices, we observe that even for this tiny example, the quantum computer makes an error. This demonstrates that existing quantum hardware still has a long way to go before becoming commercially relevant.
Does quantum computing have applications in airline revenue management?
Now, imagine in the (hopefully not too distant) future that quantum hardware matures to a level where we have access to commercially scalable and error-free quantum computers. Would there be any application for these computers in airline RM?
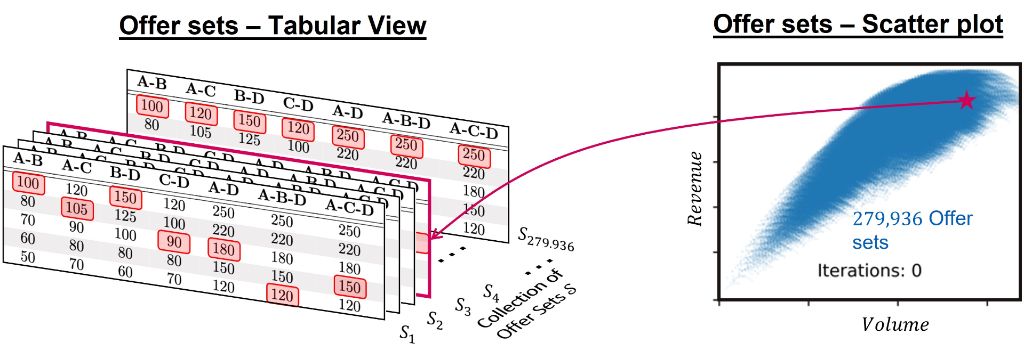
What would happen if we tried to price all the itineraries in the network simultaneously? Assume the airline can choose between 5 different fares (price points) for each of the 7 possible itineraries in the network. In Figure 3 (left), we illustrate all the possible combinations of fares – also called the offer sets – as “cards” that states the fares for each itinerary. Even in this small example, there are 279,936 cards that the airline must search amongst to find the ones that maximize the revenue. It can be shown that at most 6 cards out of the 279,936 are optimal. The problem therefore becomes how to identify the right ones.
While this may not be too difficult for this small network, consider a realistic airline network – for instance, 9 fare classes and 20 alternative itineraries connecting two cities. In this case, there is an astronomical 10^20, or 100 quintillion offer sets, which makes it impossible for a classical computer to search through them.
However, this is exactly what a quantum computer is good at!
Unlike a classical computer that searches through the offer sets sequentially, the properties of quantum computing allows us to perform the searches in parallel. In Figure 4, we can see the magic unfold. Starting initially with the cloud of 279,936 dots, we execute the quantum search algorithm. This algorithm is iterative, and we observe how successive iterations gradually make the cloud “evaporate” until only the good solutions remain.
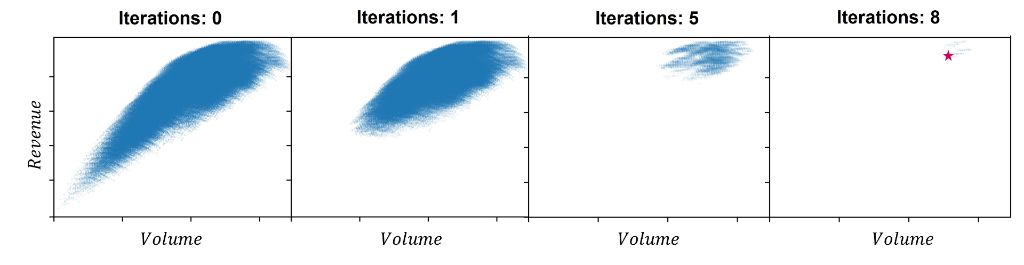
In general, one can prove that the quantum search algorithm provides a quadratic speed-up. This has dramatic consequences. Returning to the realistic sized network, the quantum speedup implies that the search can be performed 10 billion times faster! With such a speed-up it now becomes feasible to solve the itinerary choice-based network optimization within hours.
Commercially this would mean that an airline could increase its revenue by 2%-3% as was demonstrated by the researchersQian Liu and Garrett Van Ryzin in 2008 .
While the quantum technology needed for solving this problem does not exist yet, the wait may not be too long. In theroadmap
shared by IBM, one of the leading quantum hardware providers, they expect commercially viable quantum computers by 2026+. As we have demonstrated, quantum computing can solve previously unsolvable problems and provide airlines with significant revenue benefits. However, until the quantum hardware matures, the time is well spent looking for a similar quantum advantage in other areas.
TO TOP










